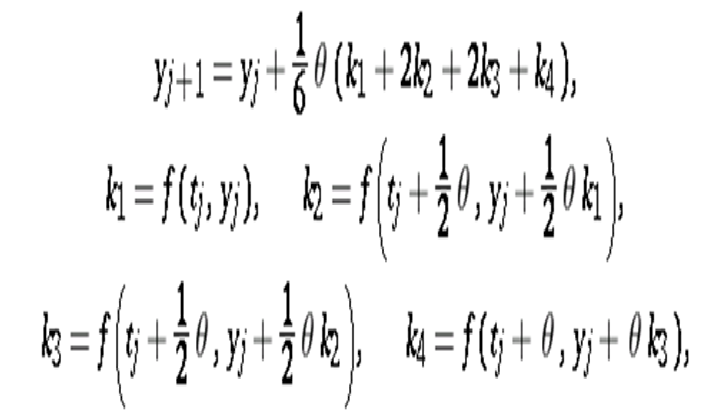
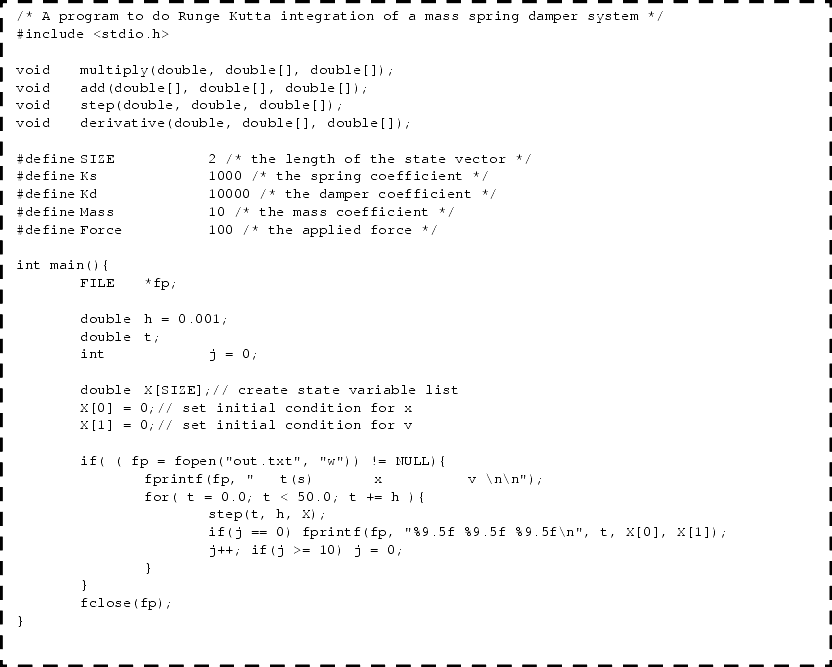
Runge-Kutta Methods – C PROGRAM. The fourth-order Runge-Kutta method uses the following formula: The program for the second-order Runge-Kutta Method is shown below. PROGRAM RUNGE_KUTTA. Biesse Rover 346 Software. Which is of type ypStepFunc and performs a single step of the fourth-order Runge-Kutta method, provided yp is of type ypFunc. Beskrajna Ljubav Jedina Je Istina Pdf.
Related Articles and Code: Program to estimate the Differential value of a given function using Runge-Kutta Methods; RUNGE-KUTTA 4th ORDER METHOD. Concurrent Rdp Patcher Windows Vista Home Premium.
Given following inputs, • An ordinary differential equation that defines value of dy/dx in the form x and y. • Initial value of y, i.e., y(0) Thus we are given below. The task is to find value of unknown function y at a given point x. The Runge-Kutta method finds approximate value of y for a given x. Only first order ordinary differential equations can be solved by using the Runge Kutta 4th order method.
Below is the formula used to compute next value y n+1 from previous value y n. The value of n are 0, 1, 2, 3,.(x – x0)/h. Here h is step height and x n+1 = x 0 + h. Lower step size means more accuracy. The formula basically computes next value y n+1 using current y n plus weighted average of four increments.
• k 1 is the increment based on the slope at the beginning of the interval, using y • k 2 is the increment based on the slope at the midpoint of the interval, using y + hk 1/2. • k 3 is again the increment based on the slope at the midpoint, using using y + hk 2/2.
• k 4 is the increment based on the slope at the end of the interval, using y + hk 3. The method is a fourth-order method, meaning that the local truncation error is on the order of O(h 5), while the total accumulated error is order O(h 4). Source: Below is implementation for the above formula. # Python program to implement Runge Kutta method # A sample differential equation 'dy / dx = (x - y)/2' def dydx(x, y): return ((x - y)/2) # Finds value of y for a given x using step size h # and initial value y0 at x0.